Implementing a 2d-tree in Clojure
Recently I followed the very good Coursera course “Algorithms, Part I” from Coursera. The exercises were in Java, and the most fun one was implementing a two-dimensional version of a k-d tree. Since I sometimes do generative art in Clojure, I thought this would be a fun algorithm to implement myself.
There already exists other implementations, for example this one, but this time I wanted to learn, not use.
What is a 2-d tree?
A 2-d tree is a spatial data structure that is efficient for nearest neighbour and range searches in a two-dimensional coordinate system.
It is a generalization of a binary search tree to two dimensions. Recall that in a binary search tree, one builds a tree structure by inserting elements such that the left nodes always are lower, and the right nodes always are higher. In that way, one only needs $O(\log(n))$ lookups to find a given element. See Wikipedia for more details.
In a 2-d tree one manages to do the same with points $(x,y)$ by alternating the comparison on the $x$ or $y$ coordinate. For each insertion, one splits the coordinate system in two.
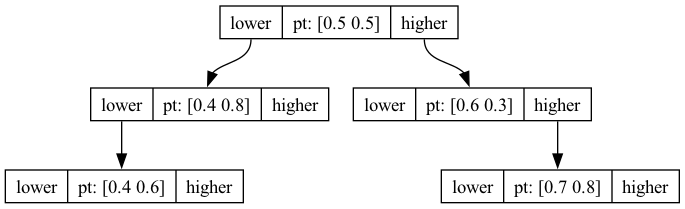
Look at the following illustration:
This is the resulting tree structure after having inserted the points $(0.5, 0.5)$, $(0.6, 0.3)$, $(0.7, 0.8)$, $(0.4, 0.8)$, and $(0.4, 0.6)$. For each level of the tree, the coordinate to compare with is alternating.
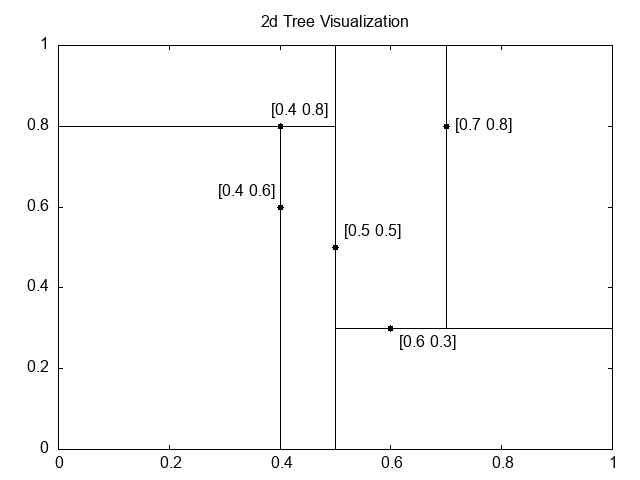
The following illustration shows how the tree divides the coordinate system into sub-regions:
To illustrate searching, let’s look up $(0.4, 0.6)$. Then we first compare it with $(0.5, 0.5)$. The $x$ coordinate is lower, so we look at the left subtree. Now the $y$ coordinate is lower, so we look at the left subtree again, and we found our point. This is 2 compares instead of the maximum 5.
There’s a lot more explanation on Wikipedia.
Implementing it in Clojure
Let’s jump straight to the implementation in Clojure. We first define a node to contain tree values: the point to insert, a boolean indicating if we are comparing vertically or horizontally (vertical means comparing the $x$-coordinate), and a rectangle, indicating which subregion the node corresponds to.
(defrecord TreeNode [value vertical rect])
(note: we don’t really need to carry around the rectangle information - it can be computed from the vertical boolean and the previous point. I might optimize this later.)
(defn- tree-cons [root pt]
(loop [path []
vertical true]
;; If the current path exists
(if-let [{:keys [value]} (get-in root path)]
(let [comparator-fn (if vertical first second)
current-compare-res (<= (comparator-fn pt) (comparator-fn value))]
(cond
;; If pt already in tree, just return the tree
(= value pt)
root
;; If pt is lower than current value, recur with :lower appended to path
current-compare-res
(recur (conj path :lower) (not vertical))
:else
(recur (conj path :higher) (not vertical))))
;; We are in the case of a non-existing node
;; If path is empty, it means the tree was nil. Return a root node.
(if (empty? path)
(assoc
(->TreeNode pt vertical (->Rectangle 0 0 1 1)) :size 1)
;; Otherwise, insert a new node at the current path
(let [{prev-pt :value prev-rect :rect} (get-in root (pop path))
curr-key (peek path)]
(-> root
(update :size inc)
(assoc-in path
(->TreeNode pt vertical
(if vertical
(if (= curr-key :lower)
(below-of prev-rect prev-pt)
(top-of prev-rect prev-pt))
(if (= curr-key :lower)
(left-of prev-rect prev-pt)
(right-of prev-rect prev-pt)))))))))))
Insertion is almost identical to insertion into a binary search tree. Where the structure shines, is when looking for nearest neighbour. The strategy is as follows: keep track of the “best so far” point, and only explore subtrees that are worth exploring.
When is a subtree wort exploring? Only when its region is closer to the search point than the current best point:
(defn- worth-exploring?
"Is the `rect` worth exploring when looking for pt?"
[rect best-so-far pt]
(< (distance-squared rect pt) (p/distance-sq pt best-so-far)))
In addition, we do one optimization when there are two subtrees. We explore the closest subtree first. Here’s the full code:
(defn- tree-nearest
"Find the nearest pt in the tree represented by root."
[root pt]
(if (nil? root) nil
(loop [best-so-far (:value root)
paths [[]]]
(let [current-path (peek paths)
{:keys [value lower higher vertical] :as current-node} (get-in root current-path)
best-so-far* (min-key #(p/distance-sq pt %) value best-so-far)]
(cond
;; The stack of paths to be explored is empty, return best-so-far
(nil? current-path)
best-so-far
;; If pt = value, then no need to do anything more
(= pt value)
value
;; Both children exist
(and lower higher)
(let [comparator-fn (if vertical first second)
current-compare-res (<= (comparator-fn pt) (comparator-fn value))
;; Explore closest node first
child-nodes (if current-compare-res '(:higher :lower) '(:lower :higher))
v (->> child-nodes
;; Filter nodes worth exploring
(transduce (comp (filter #(worth-exploring? (:rect (% current-node)) best-so-far* pt))
(map #(conj current-path %))) conj (pop paths)))]
(recur best-so-far* v))
(some? lower)
(if (worth-exploring? (:rect lower) best-so-far* pt)
(recur best-so-far* (conj (pop paths) (conj current-path :lower)))
(recur best-so-far* (pop paths)))
(some? higher)
(if (worth-exploring? (:rect higher) best-so-far* pt)
(recur best-so-far* (conj (pop paths) (conj current-path :higher)))
(recur best-so-far* (pop paths)))
:else
(recur best-so-far* (pop paths)))))))
In the recursion, we keep a stack of paths (it looks like [[:higher :lower] [:higher :higher] ...]). When exploring a new node, we add it to the top of the stack, and when recurring, we pop the current stack.
Here’s how the data structure looks after inserting the same points as in the illustration above:
{:value [0.5 0.5],
:vertical true,
:rect {:xmin 0.0, :ymin 0.0, :xmax 1.0, :ymax 1.0},
:size 5,
:higher
{:value [0.6 0.3],
:vertical false,
:rect {:xmin 0.5, :ymin 0.0, :xmax 1.0, :ymax 1.0},
:higher {:value [0.7 0.8], :vertical true, :rect {:xmin 0.5, :ymin 0.3, :xmax 1.0, :ymax 1.0}}},
:lower
{:value [0.4 0.8],
:vertical false,
:rect {:xmin 0.0, :ymin 0.0, :xmax 0.5, :ymax 1.0},
:lower {:value [0.4 0.6], :vertical true, :rect {:xmin 0.0, :ymin 0.0, :xmax 0.5, :ymax 0.8}}}}
Integrating with core Clojure functions
I wanted the tree structure to behave like a normal Clojure collection. The way to do this, is to implement the required interfaces. For example, to be able to use cons, conj, map, filter, etc, we have to implement the clojure.lang.ISeq interface. To find out which methods we need to implement, I found this Gist very helpful.
I create a new type that I call TwoTree using deftype:
(deftype TwoTree [root]
I2DTree
(value [_]
(:value root))
(intersect-rect [_ other-rect]
(tree-insersect-rect root other-rect))
(nearest [_ pt]
(tree-nearest root pt))
clojure.lang.ISeq
(first [_]
(letfn [(first* [{:keys [lower value]}]
(if lower (recur lower) value))]
(first* root)))
(cons [_ pt]
(TwoTree. (tree-cons root pt)))
(next [this]
(seq (.more this)))
(more [_]
(letfn [(more* [{:keys [lower higher] :as node} path]
(cond
lower (recur lower (conj path :lower))
(seq path) (TwoTree. (assoc-in root path higher))
:else (TwoTree. higher)))]
(more* root [])))
clojure.lang.Seqable
(seq [this]
(when (contains? root :value) this))
clojure.lang.IPersistentCollection
(equiv [this other]
(seq-equals this other))
(empty [_]
(TwoTree. nil))
clojure.lang.Counted
(count [_]
(get root :size 0))
clojure.lang.IPersistentSet
(disjoin [_ _]
(throw (Exception. "Not supported")))
(contains [this pt]
(boolean (get this pt)))
(get [_ pt]
(if (nil? root) nil
(loop [path []]
(if-let [{:keys [value ^boolean vertical]} (get-in root path)]
(let [comparator-fn (if vertical second first)
current-compare-res (<= (comparator-fn pt) (comparator-fn value))]
(cond (= value pt) value
current-compare-res
(recur (conj path :lower))
:else
(recur (conj path :higher))))
nil)))))
When implementing TwoTree, I took a lot of inspiration (and implementation) from this blog post by Nathan Wallace. Also, thanks to the Reddit user joinr for pointing out a bad equiv implementation. Here is the diff after his comments.
We can create a helper method to create new trees:
(defn two-tree [& xs]
(reduce conj (TwoTree. nil) xs))
Now we can create a new tree like this:
(two-tree [[0.3 0.4] [0.6 0.3]])
Also, the following code works:
(filter #(> (second %) 0.5) (two-tree [0.3 0.5] [0.2 0.3] [0.5 0.5] [0.7 0.8]))
(get all points whose seconds coordinate is greater than 0.5)
The full code can be seen here on Github.
Lessons learned
I did this partly to learn a simple geometric data structure, but also to make another tool in my generative art toolbox. Implementing an algorithm helps immensely when trying to understand it: I got better and better visualizing how these trees looked like.
There are two main things about Clojure I want to mention in this section: the clojure.test.check library, and the Clojure interfaces.
The clojure.test.check library
The test.check library is a property based testing library. In a few words, given constraints on inputs, in can generate test data for your function. In one particular case, it helped me verify that my code had a bug and produce a minimal example of this (the bug was that I forgot to recur in the :else clause in the tree-nearest function). By writing some “simple-ish” code, I got an example of an input that made the tree-nearest return a wrong answer. Here is the code:
(defn nearest-by-sort [pts pt]
(-> (sorted-set-by (fn [p q] (compare (p/distance-sq p pt) (p/distance-sq q pt))))
(into pts)
(first)))
(defn ^:private points-gen [min-length max-length]
(-> {:infinite? false :max 1 :NaN? false :min 0}
gen/double*
(gen/vector 2)
(gen/vector min-length max-length)))
(def prop (prop/for-all [[p & pts] (points-gen 3 50)]
(let [t (reduce conj (s/two-tree) pts)
correct-answer (nearest-by-sort pts p)
correct-dist (p/distance-sq correct-answer p)
tree-answ (s/nearest t p)
tree-dist (p/distance-sq tree-answ p)]
(= correct-dist tree-dist))))
(deftest nearest-generative
(is (= nil (let [res (tc/quick-check 10000 prop)]
(when (not (:pass? res))
(let [failed (first (:smallest (:shrunk res)))
t (reduce conj (s/two-tree) failed)
answ (nearest-by-sort failed [0.5 0.5])
tree-answ (s/nearest t [0.5 0.5])]
{:tree t
:failed failed
:root (.root t)
:tree-answ tree-answ
:tree-dist (p/distance-sq [0.5 0.5] tree-answ)
:correct-dist (p/distance-sq [0.5 0.5] answ)
:answ answ}))))))
It is probably more verbose than needed, but the summary is this: the points-gen function return a generator, which, given some restraints, can return sample inputs (in this case: vectors of points). Then I compare the result from the tree-search with the brute force result given by first sorting the points, then picking the first point.
The way I’ve set it up, whenever I run my tests, clojure.test.check generates 10000 test cases and fails the test if my implementation doesn’t return the correct result. This was very handy, and quite easy to set up.
The Clojure core interfaces
It was rewarding to implement the Clojure core interfaces for my TwoTree type (clojure.lang.ISeq, clojure.lang.IPersistentSet, etc.). What was a bit frustrating though, was the lack of documentation. I ended up reading a lot of Clojure source code to understand the control flows. Basically, the only thing I now about IPersistentSet, is that it is a Java interface like this:
package clojure.lang;
public interface IPersistentSet extends IPersistentCollection, Counted{
public IPersistentSet disjoin(Object key) ;
public boolean contains(Object key);
public Object get(Object key);
}
Then I had to search the Clojure source code to understand how it was supposed to be used. It would be nice with a docstring or two. I found many blog posts that implemented custom types (this one, this one, or this one), but very little in Clojure own documentation.
On the flip side, I got to read some of the Clojure source code, which was very educational. I also got to understand a bit more the usefulness of protocols (using defprotocol and defrecord to provide several implementations). Here it was very useful to read the source code of thi-ng/geom.
Conclusion
I learned a lot, and I got one more tool to make generative art. Perhaps later I could publish the code as a library, but I should really battle test it a bit more first (anyone can copy the code, it is open source on my Github)
I used the data structure to create the following pictures (maybe soon I’ll link to my own page instead of Instagram). The nearest function was very useful in making the code fast enough.
Until then, thanks for reading this far!